Nedoporučuji tyto poznámky používat pro vlastní potřeby. Místo toho se doporučji podívat např. na skripta pana profesora Hladíka či na skripta pana docenta Bečváře. Víc materiálu je dostupných na Matfyz wiki.
Contents
Intro
Matice
Druhy matic
Nulová matice je taková matice, která pro libovolné splňuje . Značí se též jen 0.
Jednotková matice je taková matice, která pro libovolné splňuje právě když i = j, jinak . Značí se též jen I.
Theorems
Inverzní matice splňuje, že .
Nejprve ukážeme, že je regulární. Pokud má řešení, pak .
Existuje tedy a dostáváme .
Množina všech permutací na n prvcích společně s operací skládání tvoří symetrickou grupu .
Nejprve ověříme, že operace skládání je na této množině uzavřená. Ověříme, že permutace je bijektivní:
- pro , permutace je tedy injektivní (prostá)
- , permutace je tedy surjektivní (na)
Snadno nahlédneme, že skládání permutací je zároveň asociativní. Množina všech permutací bude také obsahovat inverzní prvek () a identitu (neutrální prvek, ).
Jakoukoliv permutaci lze rozložit na transpozice.
Cyklus lze rozložit např. podle: .
Pro libovolné .
Počet inverzí . Nejprve sečteme všechny inverze v p, poté všechny inverze v q, a poté odstraníme inverze, které se vyskytují v p i q, jelikož se nám ve složené permutaci vyruší.
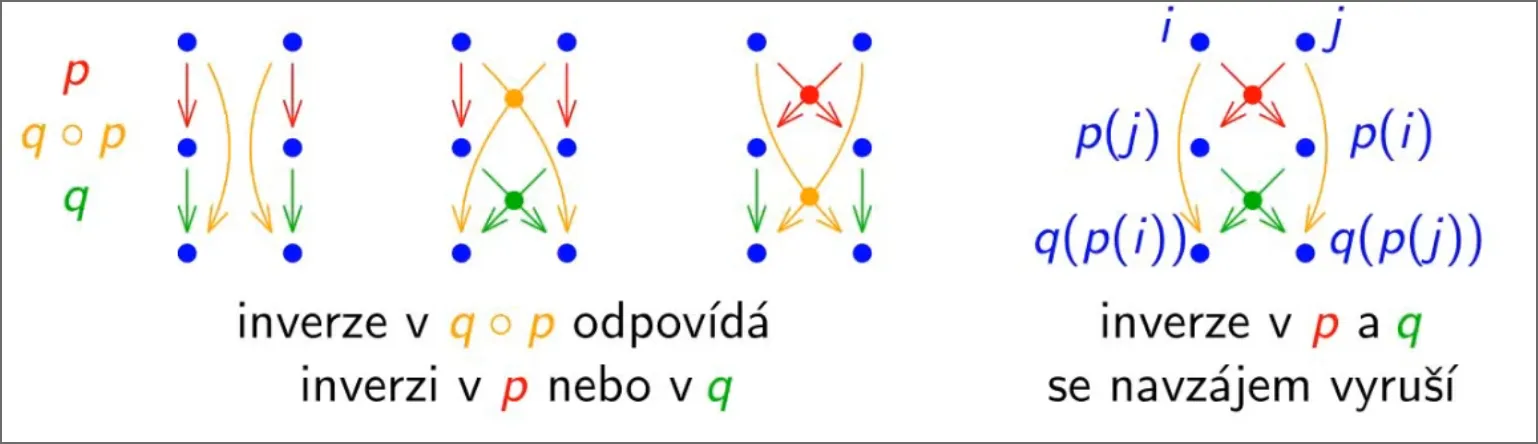
Pro .
.
Jedničku můžeme dostat buďto vynásobením dvou 1 nebo dvou -1, platí tedy, že se musí rovnat.
Tělesa
.
.
.
.
Pokud .
Pokud , jinak existuje takové, že .
Alternativně si můžeme rovnou říct, že , což je spor.
je těleso právě tehdy, když p je prvočíslo.
- Dopřednou implikaci dokážeme tím, že pokud by p bylo složené, pak . To však vede ke sporu s .
- Zpětnou implikaci dokážeme tím, že najdeme inverzní prvek ke každému prvku, čili . Nejprve najdeme takové zobrazení , takové, že . Pokud ke každému a existuje inverzní prvek, obor hodnot musí nutně obsahovat 1, jinak takový prvek neexistuje. Zobrazení tedy musí být surjektivní a jelikož je na konečné množině, musí být nutně injektivní. To dokážeme sporem: . Tedy buď se jedno z (což nejde, protože 0 se nenachází v ), nebo a i (b-c) dělí p, což je spor s tím, že p je prvočíslo (a má tedy pouze triviální dělitele).
Malá Fermatova věta: Pro prvočíslo p a .
Zobrazení je v bijektivní. Proto platí
Vektorové prostory
.
- .
- .
- .
- Alternativně si můžeme říct, že tvrdíme, že se jedná o opačný vektor, tudíž . Ověříme: .
.
Buď se a = 0, pak tvrzení platí. Pokud nikoliv, pak musí existovat .
Průnik podprostorů: Nechť je libovolný systém podprostorů prostoru V. Průnik tohoto systému je také podprostorem V.
Ověříme, že W je uzavřen na operaci součtu a násobení.
- .
- První implikace plyne z definice průniku, druhá z uzavřenosti vektorových prostorů nad součtem.
- .
- Opět první implikace plyne z definice průniku, druhá z uzavřenosti vektorových podprostorů nad skalárním součinem.
Je-li V podprostorem W konečné dimenze, pak .
Báze podprostoru V je nezávislá v prostoru W. Můžeme ji rozšířit na bázi prostoru W, avšak přitom můžeme vektory pouze přidávat, takže určitě musí platit, že .
Jsou-li U,V podprostory konečně generovaného prostoru W, pak .
Báze
Jestliže C je konečná generující množina prostoru V a B je lineárně nezávislá množina vektorů z V, pak .
Pro spor budeme předpokládat velikosti množin . Každý vektor z B si vyjádřím pomocí lineární kombinace vektorů z C (to mohu udělat, protože množina C generuje prostor V), dostanu tedy rovnici , kde B a C jsou sloupcové matice vektorů B a C. Matice A bude mít n + 1 řádků a n sloupců, má tedy jeden lineárně závislý řádek, čili původní množina B má jeden lineárně závislý vektor.
Lineární kombinace vektorů z báze B prostoru V tvořící libovolný vektor v z V je jednoznačná.
.
Věta o výměně
Nechť C generuje vektorový prostor V nad T, . Pokud lze vektor v zapsat jako lineární kombinaci vektorů z C, v níž u c je nenulový koeficient, tak množina generuje V. Formálně: .
- Následně si zapíšu jako lineární kombinaci vektorů z C, kde za dosadím výraz výše. Dostávám rovnici, kterou upravím následovně:
V poslední úpravě si uvědomím, že ve (3) mám dvě sumy, jednu rozepsanou a jednu zkrácenou. Obě však obsahují pouze , pouze s jinými koeficienty. Sepíšu je tedy do jedné sumy a dostávám upravený poslední řádek. (Pokud se učíte z prezentací pana profesora Fialy, vězte, že jeho značení je obráceně - iteruje přes j a cílové c značí indexem i.)
Nechť B je konečná lineárně nezávislá množina ve vektorovém prostoru V a C generuje V. Pak existuje D taková, že:
Dokážeme podle indukce přes . Pokud se , poté D = C. Jinak zvolíme libovolné b z B, které neleží v C, a položíme . Protože množina B’ je lineárně nezávislá, podle indukčního předpokladu existuje D’ pro B’ a C taková, že:
Následně použijeme lemma o výměně pro b a D’. Protože B je lineárně nezávislá, je . Potom splňuje všechny čtyři vlastnosti.
Je-li vektorový prostor konečně generován, pak jakoukoli lineárně nezávislou množinu lze rozšířit na bázi.
Stačí D (generující množinu) zúžit na lineárně nezávislou při zachování B.
Pokud je vektorový prostor konečně generován, pak všechny jeho báze mají stejnou mohutnost.
Mějme báze B, C prostoru V, pak
- B nezávislá, C generuje V
- C nezávislá, B generuje V